Understanding the area of a parallelogram through a geometric approach
A parallelogram is a quadrilateral with two pairs of opposite sides parallel, and the method for calculating its area is basically similar to calculating the area of a rectangle.
We'll explain the area formula for a parallelogram in detail, provide the mathematical background needed to understand it, and see how it can be applied to real-world problems.
A parallelogram is a quadrilateral with two pairs of opposite sides parallel.
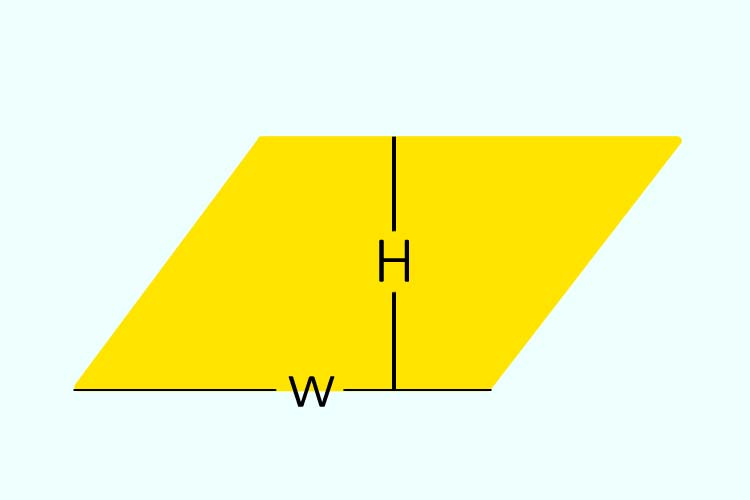
Like a rectangle, it has four sides, but they are usually not right angles.
Typical examples of parallelograms are rhombuses and rectangles.
In this case, a rectangle is a special case of a parallelogram in which all interior angles are right angles.
Characteristics of parallelogram
1. Opposite sides are parallel: Two pairs of opposite sides are parallel.
2. Length of the opposite sides: The lengths of the opposite sides are the same.
3. Diagonals: The diagonals of a parallelogram bisect each other.
4. Opposite angles: The interior angles facing each other have the same size.
5. Height: The vertical distance between the base and a pair of non-parallel opposite sides is called height.
Area formula of parallelogram
The basic formula for finding the area of a parallelogram is as follows:
\[ \text{area} = bottom \times height \]
This formula is very similar to finding the area of a rectangle.
In a rectangle, the height is perpendicular to the base, but in a parallelogram, the height is the distance perpendicular to the slanted side.
Example 1: Calculating the area of a basic parallelogram
Let's assume there is a parallelogram with a base length of 8 cm and a height of 5 cm. The area of this parallelogram can be calculated as
\[ \text{area} = 10 \, \text{cm} \times 6 \, \text{cm} = 60 \, \text{cm}^2 \]
To understand the formula for the area of a parallelogram, a geometric approach is helpful. Just like finding the area of a rectangle, you can cut a parallelogram into a rectangle.
In parallelogram ABCD, let AB be the base and AD be the height. You can convert this parallelogram to a rectangle in the following way
1. Find the height by drawing a perpendicular line from one vertex of a parallelogram.
2. Divide the parallelogram into two triangles based on this height.
3. Cut one triangle and move it to the other to make a rectangle.
Since the base and height of the converted rectangle are the same as the base and height of the original parallelogram, the area of this rectangle is the same as the area of the parallelogram.
Example 2: Convert to rectangle to find area
Suppose we have a parallelogram with a base length of 10 cm and a height of 6 cm. Converting this to a rectangle, the area of the converted rectangle is
\[ \text{area} = 10 \, \text{cm} \times 6 \, \text{cm} = 60 \, \text{cm}^2 \]
Using vectors provides another way to find the area of a parallelogram. The area of the parallelogram formed by the two vectors \(\vec{u}\) and \(\vec{v}\) is obtained as follows: can.
\[ \text{area} = |\vec{u} \times \vec{v}| \]
Here, \(\vec{u} = (3, 4)\) and \(\vec{v} = (2, -1)\) is the cross product of the two vectors. The size of the cross product represents the area of the parallelogram formed by the two vectors.
Example 3: Calculating area using vectors
Vectors \(\vec{u} = (3, 4)\) and \(\vec{v} = (2, -1)\ Let's find the area of the parallelogram formed by ). The cross product of two vectors is calculated as
\[ \vec{u} \times \vec{v} = (3 \cdot (-1) - 4 \cdot 2) = -3 - 8 = -11 \]
Therefore, the area takes the absolute value
\[ \text{area} = |-11| = 11 \]
Using vectors like this, it is also possible to calculate area using points on the coordinate plane.
Applications in real life
Calculating the area of a parallelogram is used in various fields such as architecture, engineering, and design.
For example, when calculating the area of a specific area in a building design drawing, a method is used to calculate the area of each area by dividing it into basic geometric shapes.
At this time, the formula for the area of a parallelogram is useful.
Also, in graphic design, when combining shapes of various shapes to create a desired image, it is important to accurately calculate the area of each shape.
This allows you to maintain the ratio between shapes and achieve a balanced design.
The formula for the area of a parallelogram is basically a simple formula of multiplying the base by the height.
This allows you to find the area using various methods such as geometric transformation and vector calculation.
The ability to understand the area formula of a parallelogram and apply it to real-life problems improves mathematical thinking and is a great help in solving various real-life problems.
We'll explain the area formula for a parallelogram in detail, provide the mathematical background needed to understand it, and see how it can be applied to real-world problems.
A parallelogram is a quadrilateral with two pairs of opposite sides parallel.

Like a rectangle, it has four sides, but they are usually not right angles.
Typical examples of parallelograms are rhombuses and rectangles.
In this case, a rectangle is a special case of a parallelogram in which all interior angles are right angles.
Characteristics of parallelogram
1. Opposite sides are parallel: Two pairs of opposite sides are parallel.
2. Length of the opposite sides: The lengths of the opposite sides are the same.
3. Diagonals: The diagonals of a parallelogram bisect each other.
4. Opposite angles: The interior angles facing each other have the same size.
5. Height: The vertical distance between the base and a pair of non-parallel opposite sides is called height.
Area formula of parallelogram
The basic formula for finding the area of a parallelogram is as follows:
\[ \text{area} = bottom \times height \]
This formula is very similar to finding the area of a rectangle.
In a rectangle, the height is perpendicular to the base, but in a parallelogram, the height is the distance perpendicular to the slanted side.
Example 1: Calculating the area of a basic parallelogram
Let's assume there is a parallelogram with a base length of 8 cm and a height of 5 cm. The area of this parallelogram can be calculated as
\[ \text{area} = 10 \, \text{cm} \times 6 \, \text{cm} = 60 \, \text{cm}^2 \]
To understand the formula for the area of a parallelogram, a geometric approach is helpful. Just like finding the area of a rectangle, you can cut a parallelogram into a rectangle.
In parallelogram ABCD, let AB be the base and AD be the height. You can convert this parallelogram to a rectangle in the following way
1. Find the height by drawing a perpendicular line from one vertex of a parallelogram.
2. Divide the parallelogram into two triangles based on this height.
3. Cut one triangle and move it to the other to make a rectangle.
Since the base and height of the converted rectangle are the same as the base and height of the original parallelogram, the area of this rectangle is the same as the area of the parallelogram.
Example 2: Convert to rectangle to find area
Suppose we have a parallelogram with a base length of 10 cm and a height of 6 cm. Converting this to a rectangle, the area of the converted rectangle is
\[ \text{area} = 10 \, \text{cm} \times 6 \, \text{cm} = 60 \, \text{cm}^2 \]
Using vectors provides another way to find the area of a parallelogram. The area of the parallelogram formed by the two vectors \(\vec{u}\) and \(\vec{v}\) is obtained as follows: can.
\[ \text{area} = |\vec{u} \times \vec{v}| \]
Here, \(\vec{u} = (3, 4)\) and \(\vec{v} = (2, -1)\) is the cross product of the two vectors. The size of the cross product represents the area of the parallelogram formed by the two vectors.
Example 3: Calculating area using vectors
Vectors \(\vec{u} = (3, 4)\) and \(\vec{v} = (2, -1)\ Let's find the area of the parallelogram formed by ). The cross product of two vectors is calculated as
\[ \vec{u} \times \vec{v} = (3 \cdot (-1) - 4 \cdot 2) = -3 - 8 = -11 \]
Therefore, the area takes the absolute value
\[ \text{area} = |-11| = 11 \]
Using vectors like this, it is also possible to calculate area using points on the coordinate plane.
Applications in real life
Calculating the area of a parallelogram is used in various fields such as architecture, engineering, and design.
For example, when calculating the area of a specific area in a building design drawing, a method is used to calculate the area of each area by dividing it into basic geometric shapes.
At this time, the formula for the area of a parallelogram is useful.
Also, in graphic design, when combining shapes of various shapes to create a desired image, it is important to accurately calculate the area of each shape.
This allows you to maintain the ratio between shapes and achieve a balanced design.
The formula for the area of a parallelogram is basically a simple formula of multiplying the base by the height.
This allows you to find the area using various methods such as geometric transformation and vector calculation.
The ability to understand the area formula of a parallelogram and apply it to real-life problems improves mathematical thinking and is a great help in solving various real-life problems.