Formula and example for finding the area of a rhombus
A rhombus is an important shape in planar geometry. It is a square in which all four sides have the same length and its diagonals intersect each other perpendicularly.
These properties allow the rhombus to be used in a variety of situations.
Let's learn about various methods and their theoretical background, focusing on the formula for calculating the area of a rhombus.
A rhombus is a quadrilateral with the following properties:
1. All four sides are the same length.
2. The diagonals intersect each other perpendicularly.
3. The diagonals bisect each other.
4. All angles of a rhombus have the same properties as parallelograms, and the diagonals intersect at the center of the rhombus.
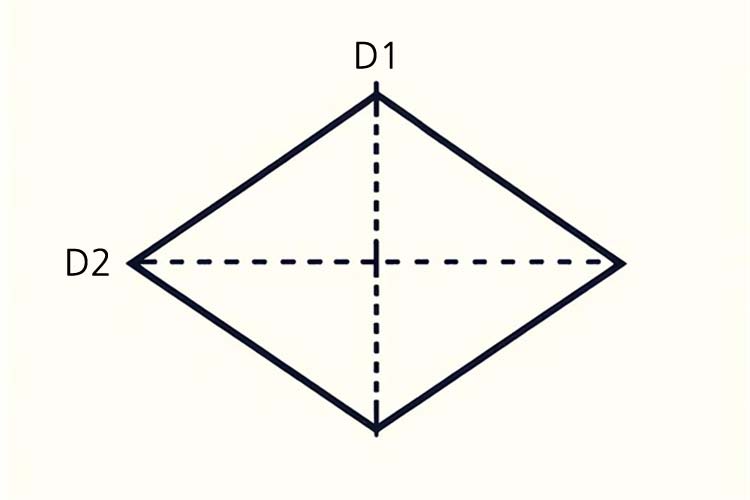
How to find the area of a rhombus
There are several formulas for finding the area of a rhombus, but the most common method is to use the length of the diagonals.
1. Area formula using diagonals
If the diagonals of a rhombus are \(d_1\) and \(d_2\), the area \(A\) can be found as follows:
\[ A = \frac{1}{2} \times d_1 \times d_2 \]
This formula comes from the fact that a rhombus can be divided into two right triangles.
Because the diagonals bisect each other perpendicularly at the center of the rhombus, the rhombus is divided into four right triangles.
The area of each right triangle is \( \frac{1}{2} \times \text{base} \times \text{height} &# You can calculate it as 92;).
Here, the base and height are each half the length of the two diagonals of the rhombus.
So, adding up the areas of all four right triangles gives us
\[ A = 4 \times \left( \frac{1}{2} \times \frac{d_1}{2} \ times \frac{d_2}{2} \right) = \frac{1}{2} \times d_1 \times d_2 \]
2. Area formula using side length and angle
When the length of the side of a rhombus is \(a\) and one interior angle is \(\theta\), the area is \(A\) can be obtained as follows:
\[ A = a^2 \sin(\theta) \]
This formula is a way to find a rhombus using trigonometric functions.
It is derived by dividing a rhombus into two triangles, finding the area of each triangle, and then adding them together.
If we divide a rhombus into two equal triangles, the area of each triangle is
\[ \text{Area of triangle} = \frac{1}{2} \times a \times a \times \sin(& #92;theta) = \frac{1}{2} a^2 \sin(\theta) \]
Therefore, adding the areas of the two triangles gives us
\[ A = 2 \times \left( \frac{1}{2} a^2 \sin(\theta) \right ) = a^2 \sin(\theta) \]
Example 1. Finding area using diagonals
Let us find the area of a rhombus whose diagonals are 6 cm and 8 cm, respectively.
Using the area formula according to the given conditions, we get
\[ A = \frac{1}{2} \times d_1 \times d_2 = \frac{1}{2} \times 6 &# 92;times 8 = 24 \text{ cm}^2 \]
So, the area of this rhombus is 24 square centimeters.
Example 2. Finding area using side length and angle
Let's find the area of a rhombus whose sides are 5cm and one interior angle is 60 degrees.
Using the area formula according to the given conditions, we get
\[ A = a^2 \sin(\theta) = 5^2 \sin(60^\circ) = 25 \times \ ;frac{\sqrt{3}}{2} \approx 21.65 \text{ cm}^2 \]
So, the area of this diamond is approximately 21.65 square centimeters.
Application of the rhombus area formula
The area formula for a rhombus is useful in a variety of real-life and geometric problems.
For example, it can be used to calculate the area of a diamond-shaped piece of land or tile.
In addition, it helps analyze and understand the properties of a rhombus through the area formula using the length of the diagonal or angle.
Additional application examples
1. Make a diamond-shaped patchwork: When using diamond-shaped pieces in patchwork or quilting, you can accurately calculate the area to determine the amount of fabric needed.
2. Architectural design: When designing a specific space in the shape of a diamond in architectural design, calculating the area helps predict material usage and calculate costs.
Due to its properties, rhombuses play an important role in a variety of geometric and real-life problems.
If you understand and use the formula for finding the area of a rhombus, you can solve problems efficiently in a variety of situations.
Area formulas using diagonals and area formulas using side lengths and angles can be useful in each situation.
These properties allow the rhombus to be used in a variety of situations.
Let's learn about various methods and their theoretical background, focusing on the formula for calculating the area of a rhombus.
A rhombus is a quadrilateral with the following properties:
1. All four sides are the same length.
2. The diagonals intersect each other perpendicularly.
3. The diagonals bisect each other.
4. All angles of a rhombus have the same properties as parallelograms, and the diagonals intersect at the center of the rhombus.

How to find the area of a rhombus
There are several formulas for finding the area of a rhombus, but the most common method is to use the length of the diagonals.
1. Area formula using diagonals
If the diagonals of a rhombus are \(d_1\) and \(d_2\), the area \(A\) can be found as follows:
\[ A = \frac{1}{2} \times d_1 \times d_2 \]
This formula comes from the fact that a rhombus can be divided into two right triangles.
Because the diagonals bisect each other perpendicularly at the center of the rhombus, the rhombus is divided into four right triangles.
The area of each right triangle is \( \frac{1}{2} \times \text{base} \times \text{height} &# You can calculate it as 92;).
Here, the base and height are each half the length of the two diagonals of the rhombus.
So, adding up the areas of all four right triangles gives us
\[ A = 4 \times \left( \frac{1}{2} \times \frac{d_1}{2} \ times \frac{d_2}{2} \right) = \frac{1}{2} \times d_1 \times d_2 \]
2. Area formula using side length and angle
When the length of the side of a rhombus is \(a\) and one interior angle is \(\theta\), the area is \(A\) can be obtained as follows:
\[ A = a^2 \sin(\theta) \]
This formula is a way to find a rhombus using trigonometric functions.
It is derived by dividing a rhombus into two triangles, finding the area of each triangle, and then adding them together.
If we divide a rhombus into two equal triangles, the area of each triangle is
\[ \text{Area of triangle} = \frac{1}{2} \times a \times a \times \sin(& #92;theta) = \frac{1}{2} a^2 \sin(\theta) \]
Therefore, adding the areas of the two triangles gives us
\[ A = 2 \times \left( \frac{1}{2} a^2 \sin(\theta) \right ) = a^2 \sin(\theta) \]
Example 1. Finding area using diagonals
Let us find the area of a rhombus whose diagonals are 6 cm and 8 cm, respectively.
Using the area formula according to the given conditions, we get
\[ A = \frac{1}{2} \times d_1 \times d_2 = \frac{1}{2} \times 6 &# 92;times 8 = 24 \text{ cm}^2 \]
So, the area of this rhombus is 24 square centimeters.
Example 2. Finding area using side length and angle
Let's find the area of a rhombus whose sides are 5cm and one interior angle is 60 degrees.
Using the area formula according to the given conditions, we get
\[ A = a^2 \sin(\theta) = 5^2 \sin(60^\circ) = 25 \times \ ;frac{\sqrt{3}}{2} \approx 21.65 \text{ cm}^2 \]
So, the area of this diamond is approximately 21.65 square centimeters.
Application of the rhombus area formula
The area formula for a rhombus is useful in a variety of real-life and geometric problems.
For example, it can be used to calculate the area of a diamond-shaped piece of land or tile.
In addition, it helps analyze and understand the properties of a rhombus through the area formula using the length of the diagonal or angle.
Additional application examples
1. Make a diamond-shaped patchwork: When using diamond-shaped pieces in patchwork or quilting, you can accurately calculate the area to determine the amount of fabric needed.
2. Architectural design: When designing a specific space in the shape of a diamond in architectural design, calculating the area helps predict material usage and calculate costs.
Due to its properties, rhombuses play an important role in a variety of geometric and real-life problems.
If you understand and use the formula for finding the area of a rhombus, you can solve problems efficiently in a variety of situations.
Area formulas using diagonals and area formulas using side lengths and angles can be useful in each situation.