Formula and application example of how to find the area of a trapezoid
A trapezoid is a quadrilateral with two parallel sides (base and top) and two slanted sides (legs).
At this time, the longer side of the two parallel sides is called the 'base side', the shorter side is called the 'top side', and the distance between the two parallel sides is called the 'height' It's called #39;.
Trapezoids have characteristics of both rectangles and parallelograms, so they often appear in a variety of mathematical and real-life problems.
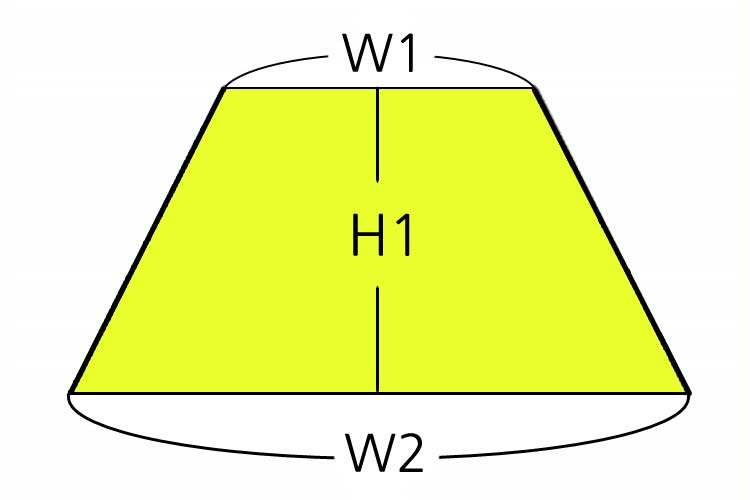
To find the area of a trapezoid, use the following formula:
\[ \text{area} = \frac{1}{2} \times (\text{bottom} + \text{top}) \times \text{height} \]
This formula is derived from the method of finding the area of a trapezoid by dividing it into two triangles and a rectangle.
Let's take a closer look at the process of deriving the area formula for a trapezoid.
Split the trapezoid into two triangles
You can divide a trapezoid into two triangles. At this time, if you find the height based on one side of the trapezoid, the height of the two triangles will be the same. You can find the area of a trapezoid by finding the areas of the two triangles and then adding them together.
Split the trapezoid into a rectangle and two triangles
Another way is to divide the trapezoid into a rectangle and two triangles. In this case, you can find the area of the trapezoid by adding the area of the rectangle and the areas of the two triangles.
1. Area of rectangle: \[ \text{bottom} \times \text{height} \]
2. Area of triangle: \[ \frac{1}{2} \times \text{bottom} \times \text{height} \]
Through these two methods, you can easily derive the formula for the area of a trapezoid.
Let's solve an example problem to help you understand the formula.
Example 1. Let’s find the area of a trapezoid whose base is 8cm long, the top side is 5cm, and the height is 4cm.
\[ \text{area} = \frac{1}{2} \times (8 + 5) \times 4 = \frac{1} {2} \times 13 \times 4 = 26 \text{cm}^2 \]
Example 2. Let’s find the area of a trapezoid whose base is 10cm long, the top side is 6cm, and the height is 5cm.
\[ \text{area} = \frac{1}{2} \times (10 + 6) \times 5 = \frac{1} {2} \times 16 \times 5 = 40 \text{cm}^2 \]
Let's look at an example of using the trapezoid area formula in practice. Calculating the area of a trapezoid is necessary in various fields such as architecture, civil engineering, and works of art.
Architecture and civil engineering
When designing a trapezoidal site or structure, calculating the exact area is very important.
For example, you can use the trapezoidal area formula to calculate the area of a slope when designing a road, or when designing a specific part of a building.
Work of art
In works of art, there are times when the area needs to be calculated when creating a trapezoid-shaped canvas or work of art.
Artists use the trapezoid area formula to balance their works and use materials appropriately.
The area formula for a trapezoid plays an important role in solving various mathematical and real-life problems.
\[ \frac{1}{2} \times (\text{bottom} + \text{top}) \times \text{height} \]
which can be useful in various fields such as architecture, civil engineering, and works of art.
Through the derivation process of this formula and example problems, we understood the basic principles of calculating the area of a trapezoid and learned how to use it in real life.
I hope you will actively use this formula when you encounter problems related to trapezoids in the future.
At this time, the longer side of the two parallel sides is called the 'base side', the shorter side is called the 'top side', and the distance between the two parallel sides is called the 'height' It's called #39;.
Trapezoids have characteristics of both rectangles and parallelograms, so they often appear in a variety of mathematical and real-life problems.

To find the area of a trapezoid, use the following formula:
\[ \text{area} = \frac{1}{2} \times (\text{bottom} + \text{top}) \times \text{height} \]
This formula is derived from the method of finding the area of a trapezoid by dividing it into two triangles and a rectangle.
Let's take a closer look at the process of deriving the area formula for a trapezoid.
Split the trapezoid into two triangles
You can divide a trapezoid into two triangles. At this time, if you find the height based on one side of the trapezoid, the height of the two triangles will be the same. You can find the area of a trapezoid by finding the areas of the two triangles and then adding them together.
Split the trapezoid into a rectangle and two triangles
Another way is to divide the trapezoid into a rectangle and two triangles. In this case, you can find the area of the trapezoid by adding the area of the rectangle and the areas of the two triangles.
1. Area of rectangle: \[ \text{bottom} \times \text{height} \]
2. Area of triangle: \[ \frac{1}{2} \times \text{bottom} \times \text{height} \]
Through these two methods, you can easily derive the formula for the area of a trapezoid.
Let's solve an example problem to help you understand the formula.
Example 1. Let’s find the area of a trapezoid whose base is 8cm long, the top side is 5cm, and the height is 4cm.
\[ \text{area} = \frac{1}{2} \times (8 + 5) \times 4 = \frac{1} {2} \times 13 \times 4 = 26 \text{cm}^2 \]
Example 2. Let’s find the area of a trapezoid whose base is 10cm long, the top side is 6cm, and the height is 5cm.
\[ \text{area} = \frac{1}{2} \times (10 + 6) \times 5 = \frac{1} {2} \times 16 \times 5 = 40 \text{cm}^2 \]
Let's look at an example of using the trapezoid area formula in practice. Calculating the area of a trapezoid is necessary in various fields such as architecture, civil engineering, and works of art.
Architecture and civil engineering
When designing a trapezoidal site or structure, calculating the exact area is very important.
For example, you can use the trapezoidal area formula to calculate the area of a slope when designing a road, or when designing a specific part of a building.
Work of art
In works of art, there are times when the area needs to be calculated when creating a trapezoid-shaped canvas or work of art.
Artists use the trapezoid area formula to balance their works and use materials appropriately.
The area formula for a trapezoid plays an important role in solving various mathematical and real-life problems.
\[ \frac{1}{2} \times (\text{bottom} + \text{top}) \times \text{height} \]
which can be useful in various fields such as architecture, civil engineering, and works of art.
Through the derivation process of this formula and example problems, we understood the basic principles of calculating the area of a trapezoid and learned how to use it in real life.
I hope you will actively use this formula when you encounter problems related to trapezoids in the future.