기하학적 접근을 통한 평행사변형의 넓이 이해하기
평행사변형은 두 쌍의 대변이 평행한 사각형으로, 넓이를 계산하는 방법은 기본적으로 직사각형의 넓이를 구하는 방법과 유사합니다.
평행사변형의 넓이 공식을 상세히 설명하고, 이를 이해하는 데 필요한 수학적 배경을 제공하며, 실제 문제에 적용하는 방법을 살펴보겠습니다.
평행사변형은 두 쌍의 대변이 각각 평행한 사각형입니다.
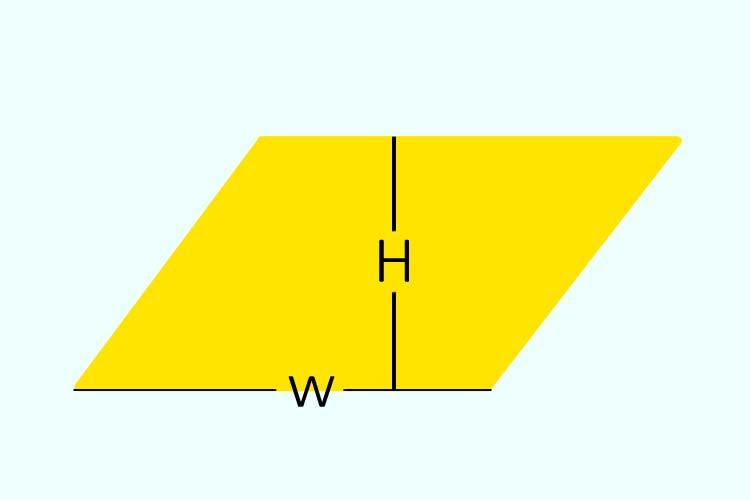
직사각형과 마찬가지로 네 개의 변을 가지고 있지만, 직각이 아닌 경우가 일반적입니다.
평행사변형의 대표적인 예로는 마름모와 직사각형이 있습니다.
이때 직사각형은 모든 내각이 직각인 특별한 경우의 평행사변형입니다.
평행사변형의 특성
1. 대변이 평행: 두 쌍의 대변이 각각 평행합니다.
2. 대변의 길이: 대변의 길이는 서로 같습니다.
3. 대각선: 평행사변형의 대각선은 서로를 이등분합니다.
4. 대각: 서로 마주 보는 내각의 크기는 같습니다.
5. 높이: 밑변과 평행하지 않은 한 쌍의 대변 사이의 수직 거리를 높이라고 합니다.
평행사변형의 넓이 공식
평행사변형의 넓이를 구하는 기본 공식은 다음과 같습니다.
\[ \text{넓이} = 밑변 \times 높이 \]
이 공식은 직사각형의 넓이를 구하는 방법과 매우 유사합니다.
직사각형에서는 높이가 밑변에 수직으로 교차하지만, 평행사변형에서는 기울어진 변과 수직인 거리가 높이가 됩니다.
예제 1: 기본적인 평행사변형의 넓이 계산
밑변의 길이가 8cm이고, 높이가 5cm인 평행사변형이 있다고 가정해봅시다. 이 평행사변형의 넓이는 다음과 같이 계산할 수 있습니다.
\[ \text{넓이} = 10 \, \text{cm} \times 6 \, \text{cm} = 60 \, \text{cm}^2 \]
평행사변형의 넓이 공식을 이해하려면 기하학적인 접근이 도움이 됩니다. 직사각형의 넓이를 구할 때처럼, 평행사변형을 잘라서 직사각형으로 만들 수 있습니다.
평행사변형 ABCD에서 AB를 밑변, AD를 높이라고 가정합니다. 이 평행사변형을 다음과 같은 방법으로 직사각형으로 변환할 수 있습니다.
1. 평행사변형의 한 꼭짓점에서 수선을 내려 높이를 구합니다.
2. 이 높이를 기준으로 평행사변형을 두 개의 삼각형으로 나눕니다.
3. 한 삼각형을 잘라서 다른 쪽으로 옮기면 직사각형이 됩니다.
이렇게 변환한 직사각형의 밑변과 높이는 원래 평행사변형의 밑변과 높이와 동일하므로, 이 직사각형의 넓이는 평행사변형의 넓이와 같습니다.
예제 2: 직사각형으로 변환하여 넓이 구하기
밑변의 길이가 10cm, 높이가 6cm인 평행사변형이 있다고 가정합니다. 이를 직사각형으로 변환하면, 변환된 직사각형의 넓이는 다음과 같습니다.
\[ \text{넓이} = 10 \, \text{cm} \times 6 \, \text{cm} = 60 \, \text{cm}^2 \]
벡터를 사용하면 평행사변형의 넓이를 구하는 또 다른 방법을 제시할 수 있습니다. 두 벡터 \(\vec{u}\)와 \(\vec{v}\) 가 이루는 평행사변형의 넓이는 다음과 같이 구할 수 있습니다.
\[ \text{넓이} = |\vec{u} \times \vec{v}| \]
여기서 \(\vec{u} \times \vec{v}\)는 두 벡터의 외적(cross product)입니다. 외적의 크기는 두 벡터가 이루는 평행사변형의 넓이를 나타냅니다.
예제 3: 벡터를 이용한 넓이 계산
벡터 \(\vec{u} = (3, 4)\) 와 \(\vec{v} = (2, -1)\) 가 이루는 평행사변형의 넓이를 구해봅시다. 두 벡터의 외적은 다음과 같이 계산됩니다.
\[ \vec{u} \times \vec{v} = (3 \cdot (-1) - 4 \cdot 2) = -3 - 8 = -11 \]
따라서 넓이는 절대값을 취하여
\[ \text{넓이} = |-11| = 11 \]
이와 같이 벡터를 사용하면 좌표평면 상의 점들을 이용한 넓이 계산도 가능합니다.
실생활에서의 응용
평행사변형의 넓이 계산은 건축, 공학, 디자인 등 다양한 분야에서 활용됩니다.
예를 들어, 건축물의 설계 도면에서 특정 구역의 면적을 계산할 때, 기초적인 기하학적 도형으로 분할하여 각각의 넓이를 계산하는 방법을 사용합니다.
이때 평행사변형의 넓이 공식은 유용하게 쓰입니다.
또한 그래픽 디자인에서도 다양한 모양의 도형을 조합하여 원하는 이미지를 만들 때, 각 도형의 넓이를 정확히 계산하는 것이 중요합니다.
이를 통해 도형 간의 비율을 유지하고, 균형 잡힌 디자인을 구현할 수 있습니다.
평행사변형의 넓이 공식은 기본적으로 밑변과 높이를 곱하는 단순한 공식입니다.
이를 통해 기하학적 변환, 벡터 계산 등의 다양한 방법을 활용하여 넓이를 구할 수 있습니다.
평행사변형의 넓이 공식을 이해하고 실제 문제에 적용하는 능력은 수학적 사고력을 향상시키고, 실생활의 다양한 문제를 해결하는 데 큰 도움이 됩니다.
평행사변형의 넓이 공식을 상세히 설명하고, 이를 이해하는 데 필요한 수학적 배경을 제공하며, 실제 문제에 적용하는 방법을 살펴보겠습니다.
평행사변형은 두 쌍의 대변이 각각 평행한 사각형입니다.

직사각형과 마찬가지로 네 개의 변을 가지고 있지만, 직각이 아닌 경우가 일반적입니다.
평행사변형의 대표적인 예로는 마름모와 직사각형이 있습니다.
이때 직사각형은 모든 내각이 직각인 특별한 경우의 평행사변형입니다.
평행사변형의 특성
1. 대변이 평행: 두 쌍의 대변이 각각 평행합니다.
2. 대변의 길이: 대변의 길이는 서로 같습니다.
3. 대각선: 평행사변형의 대각선은 서로를 이등분합니다.
4. 대각: 서로 마주 보는 내각의 크기는 같습니다.
5. 높이: 밑변과 평행하지 않은 한 쌍의 대변 사이의 수직 거리를 높이라고 합니다.
평행사변형의 넓이 공식
평행사변형의 넓이를 구하는 기본 공식은 다음과 같습니다.
\[ \text{넓이} = 밑변 \times 높이 \]
이 공식은 직사각형의 넓이를 구하는 방법과 매우 유사합니다.
직사각형에서는 높이가 밑변에 수직으로 교차하지만, 평행사변형에서는 기울어진 변과 수직인 거리가 높이가 됩니다.
예제 1: 기본적인 평행사변형의 넓이 계산
밑변의 길이가 8cm이고, 높이가 5cm인 평행사변형이 있다고 가정해봅시다. 이 평행사변형의 넓이는 다음과 같이 계산할 수 있습니다.
\[ \text{넓이} = 10 \, \text{cm} \times 6 \, \text{cm} = 60 \, \text{cm}^2 \]
평행사변형의 넓이 공식을 이해하려면 기하학적인 접근이 도움이 됩니다. 직사각형의 넓이를 구할 때처럼, 평행사변형을 잘라서 직사각형으로 만들 수 있습니다.
평행사변형 ABCD에서 AB를 밑변, AD를 높이라고 가정합니다. 이 평행사변형을 다음과 같은 방법으로 직사각형으로 변환할 수 있습니다.
1. 평행사변형의 한 꼭짓점에서 수선을 내려 높이를 구합니다.
2. 이 높이를 기준으로 평행사변형을 두 개의 삼각형으로 나눕니다.
3. 한 삼각형을 잘라서 다른 쪽으로 옮기면 직사각형이 됩니다.
이렇게 변환한 직사각형의 밑변과 높이는 원래 평행사변형의 밑변과 높이와 동일하므로, 이 직사각형의 넓이는 평행사변형의 넓이와 같습니다.
예제 2: 직사각형으로 변환하여 넓이 구하기
밑변의 길이가 10cm, 높이가 6cm인 평행사변형이 있다고 가정합니다. 이를 직사각형으로 변환하면, 변환된 직사각형의 넓이는 다음과 같습니다.
\[ \text{넓이} = 10 \, \text{cm} \times 6 \, \text{cm} = 60 \, \text{cm}^2 \]
벡터를 사용하면 평행사변형의 넓이를 구하는 또 다른 방법을 제시할 수 있습니다. 두 벡터 \(\vec{u}\)와 \(\vec{v}\) 가 이루는 평행사변형의 넓이는 다음과 같이 구할 수 있습니다.
\[ \text{넓이} = |\vec{u} \times \vec{v}| \]
여기서 \(\vec{u} \times \vec{v}\)는 두 벡터의 외적(cross product)입니다. 외적의 크기는 두 벡터가 이루는 평행사변형의 넓이를 나타냅니다.
예제 3: 벡터를 이용한 넓이 계산
벡터 \(\vec{u} = (3, 4)\) 와 \(\vec{v} = (2, -1)\) 가 이루는 평행사변형의 넓이를 구해봅시다. 두 벡터의 외적은 다음과 같이 계산됩니다.
\[ \vec{u} \times \vec{v} = (3 \cdot (-1) - 4 \cdot 2) = -3 - 8 = -11 \]
따라서 넓이는 절대값을 취하여
\[ \text{넓이} = |-11| = 11 \]
이와 같이 벡터를 사용하면 좌표평면 상의 점들을 이용한 넓이 계산도 가능합니다.
실생활에서의 응용
평행사변형의 넓이 계산은 건축, 공학, 디자인 등 다양한 분야에서 활용됩니다.
예를 들어, 건축물의 설계 도면에서 특정 구역의 면적을 계산할 때, 기초적인 기하학적 도형으로 분할하여 각각의 넓이를 계산하는 방법을 사용합니다.
이때 평행사변형의 넓이 공식은 유용하게 쓰입니다.
또한 그래픽 디자인에서도 다양한 모양의 도형을 조합하여 원하는 이미지를 만들 때, 각 도형의 넓이를 정확히 계산하는 것이 중요합니다.
이를 통해 도형 간의 비율을 유지하고, 균형 잡힌 디자인을 구현할 수 있습니다.
평행사변형의 넓이 공식은 기본적으로 밑변과 높이를 곱하는 단순한 공식입니다.
이를 통해 기하학적 변환, 벡터 계산 등의 다양한 방법을 활용하여 넓이를 구할 수 있습니다.
평행사변형의 넓이 공식을 이해하고 실제 문제에 적용하는 능력은 수학적 사고력을 향상시키고, 실생활의 다양한 문제를 해결하는 데 큰 도움이 됩니다.