사다리꼴 넓이 구하는 방법 공식과 응용 예제
사다리꼴은 두 개의 평행한 변(밑변과 윗변)과 두 개의 기울어진 변(다리)을 가진 사각형입니다.
이때 평행한 두 변 중 더 긴 변을 '밑변', 더 짧은 변을 '윗변'이라 부르며, 두 평행한 변 사이의 거리를 '높이'라고 합니다.
사다리꼴은 직사각형과 평행사변형의 특성을 모두 가지고 있어, 다양한 수학적 문제와 실생활 문제에서 자주 등장합니다.
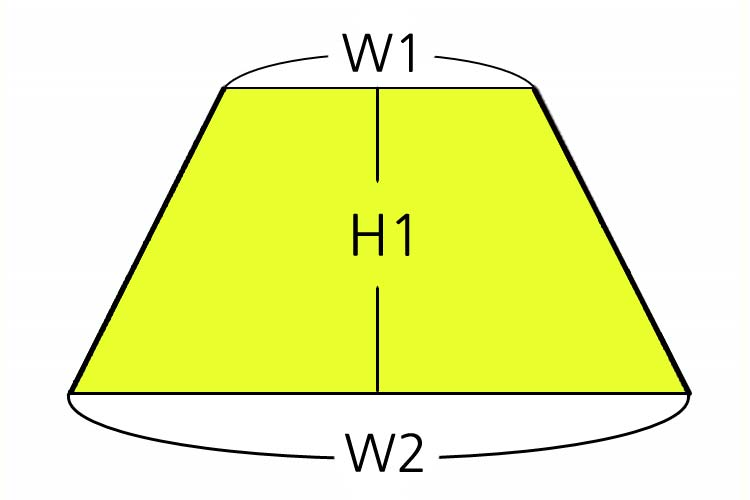
사다리꼴의 넓이를 구하기 위해서는 다음과 같은 공식을 사용합니다:
\[ \text{넓이} = \frac{1}{2} \times (\text{밑변} + \text{윗변}) \times \text{높이} \]
이 공식은 사다리꼴을 두 개의 삼각형과 하나의 직사각형으로 나누어 넓이를 구하는 방법에서 유도된 것입니다.
사다리꼴의 넓이 공식을 유도하는 과정을 자세히 살펴보겠습니다.
사다리꼴을 두 개의 삼각형으로 분할
사다리꼴을 두 개의 삼각형으로 나눌 수 있습니다. 이 때, 사다리꼴의 한 변을 기준으로 높이를 구하면 두 삼각형의 높이는 동일하게 됩니다. 두 삼각형의 넓이를 각각 구한 후 더하면 사다리꼴의 넓이를 구할 수 있습니다.
사다리꼴을 직사각형과 두 개의 삼각형으로 분할
사다리꼴을 직사각형과 두 개의 삼각형으로 나누는 방법도 있습니다. 이 경우, 직사각형의 넓이와 두 삼각형의 넓이를 더하면 사다리꼴의 넓이를 구할 수 있습니다.
1. 직사각형의 넓이: \[ \text{밑변} \times \text{높이} \]
2. 삼각형의 넓이: \[ \frac{1}{2} \times \text{밑변} \times \text{높이} \]
이 두 가지 방법을 통해 사다리꼴의 넓이 공식을 쉽게 유도할 수 있습니다.
공식의 이해를 돕기 위해 예제 문제를 풀어보겠습니다.
예제 1. 밑변의 길이가 8cm, 윗변의 길이가 5cm, 높이가 4cm인 사다리꼴의 넓이를 구해봅시다.
\[ \text{넓이} = \frac{1}{2} \times (8 + 5) \times 4 = \frac{1}{2} \times 13 \times 4 = 26 \text{cm}^2 \]
예제 2. 밑변의 길이가 10cm, 윗변의 길이가 6cm, 높이가 5cm인 사다리꼴의 넓이를 구해봅시다.
\[ \text{넓이} = \frac{1}{2} \times (10 + 6) \times 5 = \frac{1}{2} \times 16 \times 5 = 40 \text{cm}^2 \]
사다리꼴 넓이 공식을 실제로 활용하는 예시를 살펴보겠습니다. 건축, 토목 공사, 예술 작품 등의 다양한 분야에서 사다리꼴의 넓이를 계산하는 일이 필요합니다.
건축과 토목 공사
사다리꼴 형태의 부지나 구조물을 설계할 때 정확한 넓이를 계산하는 것은 매우 중요합니다.
예를 들어, 도로 설계 시 경사면의 넓이를 계산하거나, 건물의 특정 부분을 설계할 때 사다리꼴 넓이 공식을 사용할 수 있습니다.
예술 작품
예술 작품에서도 사다리꼴 형태의 캔버스나 작품을 제작할 때 넓이를 계산해야 하는 경우가 있습니다.
예술가들은 사다리꼴 넓이 공식을 활용하여 작품의 균형을 맞추고, 재료를 적절히 사용합니다.
사다리꼴의 넓이 공식은 다양한 수학적 문제와 실생활 문제를 해결하는 데 중요한 역할을 합니다.
\[ \frac{1}{2} \times (\text{밑변} + \text{윗변}) \times \text{높이} \]
라는 공식을 통해 사다리꼴의 넓이를 쉽게 계산할 수 있으며, 이를 통해 건축, 토목 공사, 예술 작품 등 다양한 분야에서 유용하게 활용할 수 있습니다.
이 공식의 유도 과정과 예제 문제를 통해 사다리꼴 넓이 계산의 기본 원리를 이해하고, 실생활에서 이를 활용하는 방법을 알아보았습니다.
앞으로 사다리꼴과 관련된 문제를 만날 때 이 공식을 적극적으로 활용해보시기 바랍니다.
이때 평행한 두 변 중 더 긴 변을 '밑변', 더 짧은 변을 '윗변'이라 부르며, 두 평행한 변 사이의 거리를 '높이'라고 합니다.
사다리꼴은 직사각형과 평행사변형의 특성을 모두 가지고 있어, 다양한 수학적 문제와 실생활 문제에서 자주 등장합니다.

사다리꼴의 넓이를 구하기 위해서는 다음과 같은 공식을 사용합니다:
\[ \text{넓이} = \frac{1}{2} \times (\text{밑변} + \text{윗변}) \times \text{높이} \]
이 공식은 사다리꼴을 두 개의 삼각형과 하나의 직사각형으로 나누어 넓이를 구하는 방법에서 유도된 것입니다.
사다리꼴의 넓이 공식을 유도하는 과정을 자세히 살펴보겠습니다.
사다리꼴을 두 개의 삼각형으로 분할
사다리꼴을 두 개의 삼각형으로 나눌 수 있습니다. 이 때, 사다리꼴의 한 변을 기준으로 높이를 구하면 두 삼각형의 높이는 동일하게 됩니다. 두 삼각형의 넓이를 각각 구한 후 더하면 사다리꼴의 넓이를 구할 수 있습니다.
사다리꼴을 직사각형과 두 개의 삼각형으로 분할
사다리꼴을 직사각형과 두 개의 삼각형으로 나누는 방법도 있습니다. 이 경우, 직사각형의 넓이와 두 삼각형의 넓이를 더하면 사다리꼴의 넓이를 구할 수 있습니다.
1. 직사각형의 넓이: \[ \text{밑변} \times \text{높이} \]
2. 삼각형의 넓이: \[ \frac{1}{2} \times \text{밑변} \times \text{높이} \]
이 두 가지 방법을 통해 사다리꼴의 넓이 공식을 쉽게 유도할 수 있습니다.
공식의 이해를 돕기 위해 예제 문제를 풀어보겠습니다.
예제 1. 밑변의 길이가 8cm, 윗변의 길이가 5cm, 높이가 4cm인 사다리꼴의 넓이를 구해봅시다.
\[ \text{넓이} = \frac{1}{2} \times (8 + 5) \times 4 = \frac{1}{2} \times 13 \times 4 = 26 \text{cm}^2 \]
예제 2. 밑변의 길이가 10cm, 윗변의 길이가 6cm, 높이가 5cm인 사다리꼴의 넓이를 구해봅시다.
\[ \text{넓이} = \frac{1}{2} \times (10 + 6) \times 5 = \frac{1}{2} \times 16 \times 5 = 40 \text{cm}^2 \]
사다리꼴 넓이 공식을 실제로 활용하는 예시를 살펴보겠습니다. 건축, 토목 공사, 예술 작품 등의 다양한 분야에서 사다리꼴의 넓이를 계산하는 일이 필요합니다.
건축과 토목 공사
사다리꼴 형태의 부지나 구조물을 설계할 때 정확한 넓이를 계산하는 것은 매우 중요합니다.
예를 들어, 도로 설계 시 경사면의 넓이를 계산하거나, 건물의 특정 부분을 설계할 때 사다리꼴 넓이 공식을 사용할 수 있습니다.
예술 작품
예술 작품에서도 사다리꼴 형태의 캔버스나 작품을 제작할 때 넓이를 계산해야 하는 경우가 있습니다.
예술가들은 사다리꼴 넓이 공식을 활용하여 작품의 균형을 맞추고, 재료를 적절히 사용합니다.
사다리꼴의 넓이 공식은 다양한 수학적 문제와 실생활 문제를 해결하는 데 중요한 역할을 합니다.
\[ \frac{1}{2} \times (\text{밑변} + \text{윗변}) \times \text{높이} \]
라는 공식을 통해 사다리꼴의 넓이를 쉽게 계산할 수 있으며, 이를 통해 건축, 토목 공사, 예술 작품 등 다양한 분야에서 유용하게 활용할 수 있습니다.
이 공식의 유도 과정과 예제 문제를 통해 사다리꼴 넓이 계산의 기본 원리를 이해하고, 실생활에서 이를 활용하는 방법을 알아보았습니다.
앞으로 사다리꼴과 관련된 문제를 만날 때 이 공식을 적극적으로 활용해보시기 바랍니다.